Overview: Astrophysical Modelling and Computation

Lecturer: Dr. Hakim L. Malasan

🌌 Filosofi Dasar: Modelling & Computation

Inti dari pemodelan dan komputasi adalah bagaimana menyelesaikan masalah-masalah sains yang sesungguhnya dengan menggunakan originalitas kita untuk membangun metode terbaik.

Apa itu Computer Experiment?

Computer experiment atau numerical experiment adalah pendekatan di mana kita menggunakan model matematis untuk mensimulasikan perilaku sistem fisis yang kompleks melalui komputasi.

🤔 Mengapa Kita Butuh Computer Experiment?

Ada tiga alasan utama mengapa eksperimen numerik sangat penting dalam astrofisika:

1. Desain Sistem Kompleks

Membantu mendesain perangkat atau sistem yang kompleks sebelum menggunakan teknologi mahal untuk membuatnya. Ini menghemat biaya dan waktu dalam tahap pengembangan.

2. Sistem yang Tidak Bisa Dieksperimen Langsung

Mendapatkan informasi tentang sistem fisis yang tidak memungkinkan untuk melakukan eksperimen di laboratorium—seperti galaksi, black hole, atau evolusi bintang yang memakan waktu jutaan tahun.

3. Memahami Sistem Kompleks

Membantu kita memahami sistem yang sangat kompleks dengan banyak variabel yang saling berinteraksi, seperti dinamika cluster bintang atau interaksi antar galaksi.

🌠 Sistem Dinamis dalam Astrofisika

Sistem dinamis adalah sistem yang berevolusi seiring waktu. Contoh klasik adalah galaksi yang memiliki:

• 3 koordinat posisi (x, y, z) - objek 3D dalam ruang
• 3 koordinat kecepatan (vx, vy, vz) - karena bisa bergerak ke segala arah

Tantangan Observasi

Ketika kita mengamati objek-objek langit dari Bumi, medan pandang kita terbatas pada sistem 2D karena kita hanya bisa melihat proyeksi objek yang sejajar dengan garis pandang kita.

Inilah mengapa komputer sangat penting: untuk melakukan simulasi dan menghitung struktur 3D yang mendasari alam semesta, yang tidak bisa kita amati langsung.

⚙️ Setting Up a Numerical Experiment

Berikut langkah-langkah umum dalam menyiapkan eksperimen numerik:

1. Fenomena Fisis 🌌

Memilih sistem fisis yang ingin diobservasi dan dipelajari.

2. Model Matematis 📐

Sistem fisis didekati dengan model matematis. Umumnya menggunakan beberapa asumsi sederhana untuk menggambarkan kerja dari sistem fisis tersebut.

3. Diskritisasi Model 🔢

Di alam, model matematis bekerja pada sistem kontinu (continuous), sedangkan komputer bekerja pada sistem diskrit (discrete).

Diperlukan konversi model matematis dalam bentuk kontinu (persamaan diferensial) ke bentuk diskrit dengan pendekatan aljabar yang bisa ditangani oleh komputer.

⚠️ Perhatian: Tahap ini harus dilakukan dengan hati-hati untuk meminimalkan kesalahan. Diskritisasi waktu dan ruang dapat menghasilkan error numerik yang besar.

4. Numerical Algorithm 🧮

Memilih algoritma numerik yang sesuai untuk menyelesaikan masalah yang dibutuhkan.

5. Computer Program 💻

Menulis code yang dibutuhkan dengan: - Optimalisasi resources - Mudah digunakan - Mudah dimodifikasi

6. Computer Experiment 🚀

Running program dan menganalisis hasil. Penting untuk mengetahui: - Apa yang di-test - Apa yang ingin ditemukan - Bagaimana menganalisis data dari hasil eksperimen

🔬 Dynamic Simulation dalam Astronomi

Terdapat banyak sistem astronomi yang dapat dimodelkan menggunakan code komputer. Kita akan fokus pada simulasi dinamis, yaitu mempelajari sistem yang berevolusi dari waktu ke waktu.

Pada banyak sistem astrofisika, properti yang paling fundamental adalah gaya gravitasi.

Contoh Aplikasi:

🪐 Sistem Tata Surya

• Dinamika dan stabilitas sistem tata surya
• Pergerakan dan interaksi asteroid pada sabuk asteroid
• Pemodelan cincin planet
• Perhitungan orbit planet

⭐ Sistem Bintang

• Formasi bintang melalui keruntuhan awan molekuler raksasa
• Dinamika sistem binary dan cluster kecil bintang
• Formasi dan evolusi cluster globular

🌌 Sistem Galaksi

• Dinamika galaksi spiral
• Interaksi antar galaksi dan penggabungan (galaxy merger)
• Evolusi galaksi

🌍 Studi Kosmologis

• Formasi struktur di alam semesta
• Masalah materi gelap (dark matter)
• Evolusi alam semesta

📊 Model Matematis: Dua Komponen Utama

Code simulasi astrofisika terdiri dari dua bagian utama:

1. Kalkulasi Gaya - Menghitung gaya yang bekerja pada setiap objek
2. Evolusi Waktu - Menghitung bagaimana sistem berubah seiring waktu

Kedua komponen ini dapat dideskripsikan oleh model matematis berupa sekumpulan persamaan matematika untuk memprediksi keadaan masa depan dari sistem ketika diberikan kondisi awal tertentu.

🎯 Gaya Gravitasi: Fondasi Simulasi

Hukum Gravitasi Newton untuk Dua Benda

Hukum universal gravitasi Newton menyatakan bahwa gaya gravitasi antara dua benda adalah:

Di mana: - \(F\) = gaya gravitasi (Newton) - \(G\) = konstanta gravitasi universal (\(6.674 \times 10^{-11}\) m³/kg·s²) - \(m_1\) = massa benda pertama (kg) - \(m_2\) = massa benda kedua (kg) - \(r\) = jarak antara kedua benda (m)

Sifat Gaya Gravitasi

Dalam bentuk vektor, gaya gravitasi antara dua benda dapat ditulis:

Ini menunjukkan bahwa gaya gravitasi adalah aksi-reaksi dengan besar yang sama tetapi arah berlawanan.

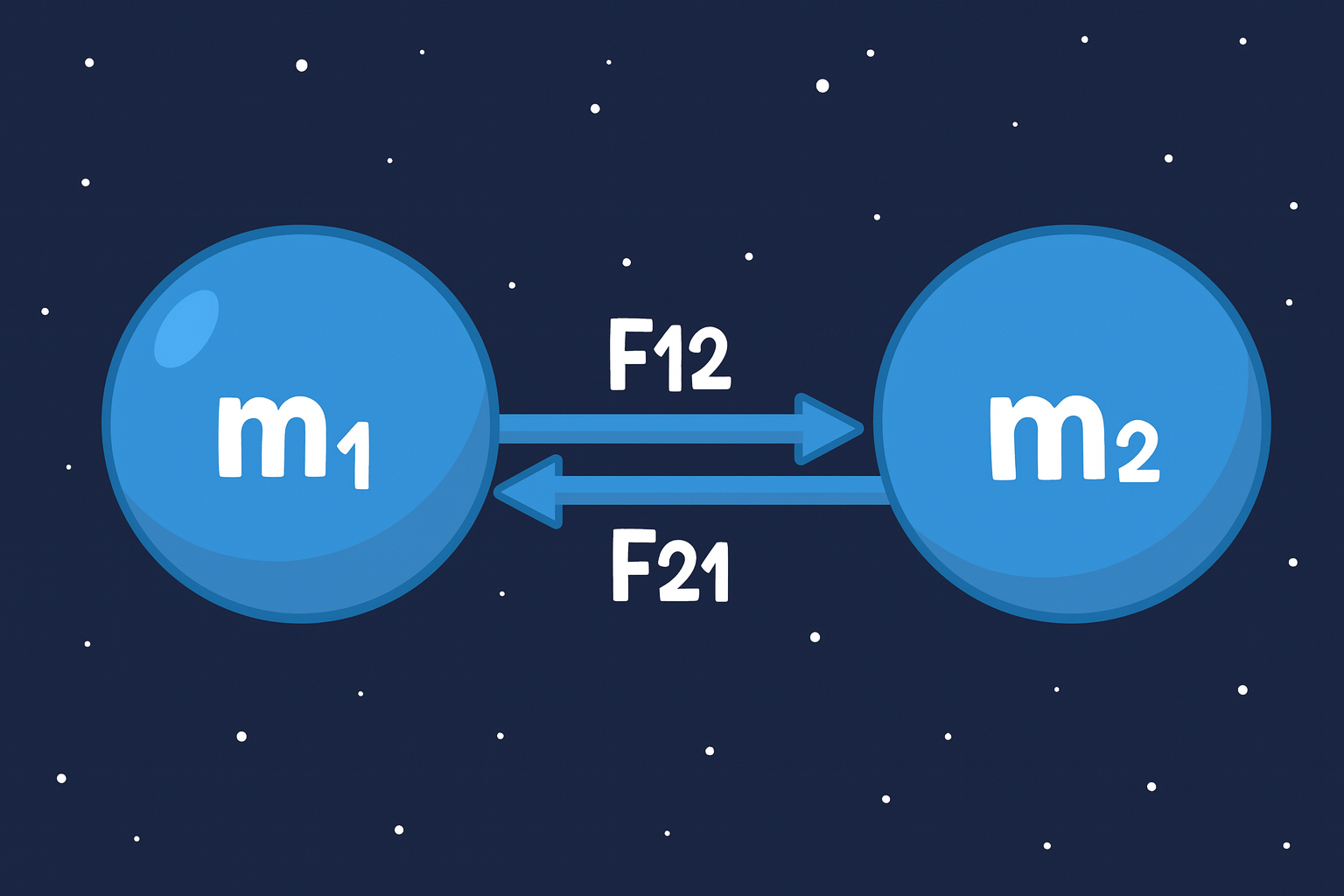
Ilustrasi gaya gravitasi antara dua benda

🔢 N-Body Problem: Sistem dengan Banyak Massa

Bagaimana jika kita memiliki lebih dari dua massa? Misalnya 5 massa yang saling berinteraksi?

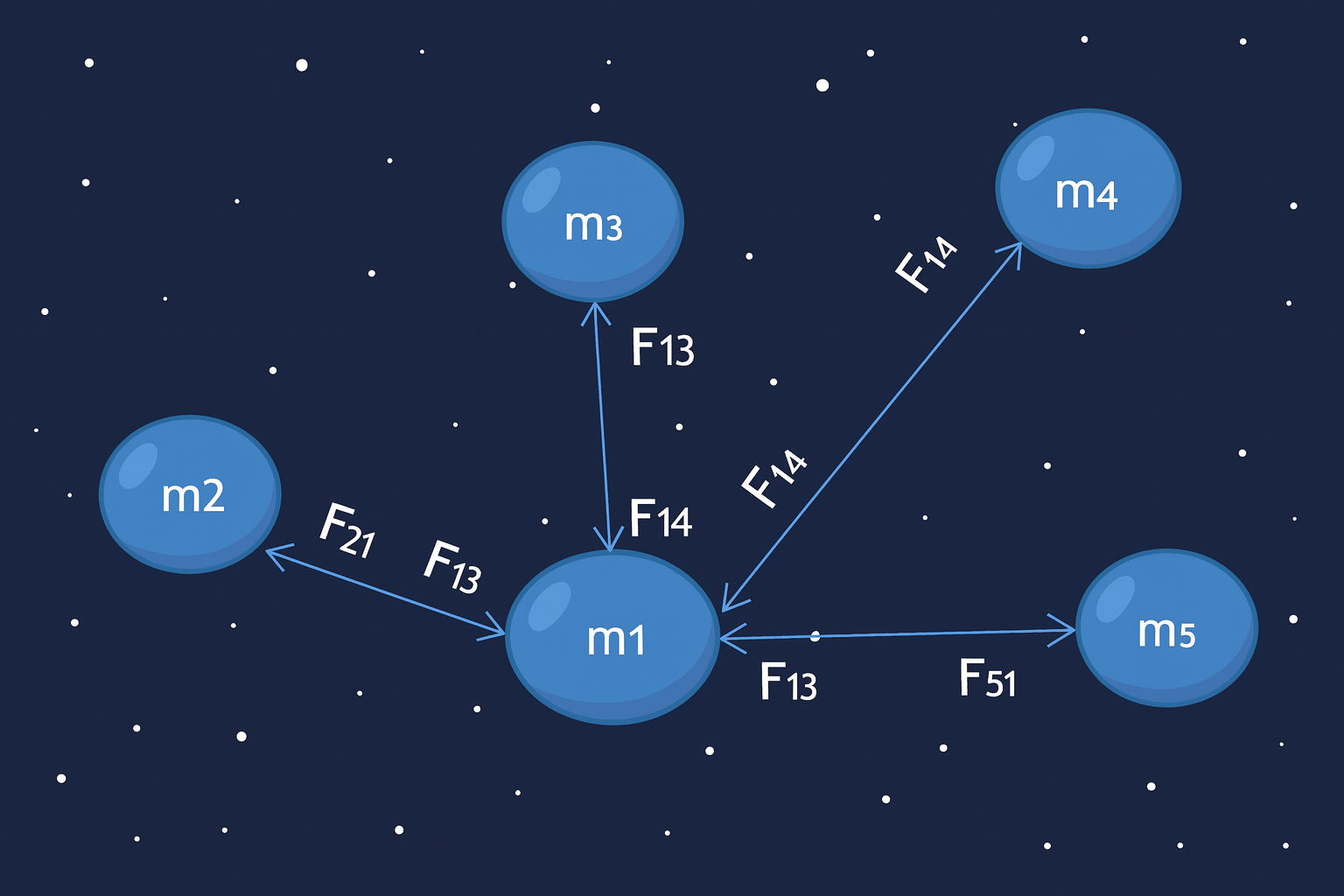
Ilustrasi gaya gravitasi dalam sistem N-body dengan 5 massa

Gaya Total pada Satu Benda

Gaya total yang bekerja pada benda ke-1 adalah jumlah vektor dari semua gaya yang diterima dari benda lainnya:

Formula Umum untuk N Benda

Secara umum, gaya gravitasi total pada benda ke-\(i\) dalam sistem N-body adalah:

Di mana: - \(\vec{F}_i\) = gaya total pada benda ke-\(i\) - \(N\) = jumlah total benda dalam sistem - \(r_{ij}\) = jarak antara benda \(i\) dan \(j\) - \(\hat{r}_{ij}\) = vektor satuan dari benda \(i\) ke benda \(j\)

⚠️ Perhatian: Singularitas Numerik

Masalah: Jika dua benda sangat dekat (\(r \to 0\)), gaya gravitasi akan mendekati tak hingga, dan komputer akan mengalami error (division by zero).

Solusi: Gunakan softening parameter \(\epsilon\):

Di mana \(\epsilon\) mewakili nilai yang sangat kecil mendekati nol untuk mencegah singularitas.

🏃 Persamaan Gerak: Evolusi Sistem

Evolusi dari sistem digambarkan oleh persamaan gerak yang menjelaskan bagaimana sistem berevolusi seiring waktu.

Definisi Kinematika

Percepatan didefinisikan sebagai laju perubahan kecepatan:

Kecepatan adalah laju perubahan posisi:

Diskritisasi untuk Komputer

Untuk implementasi di komputer, persamaan kontinu di atas didiskritisasi menjadi:

Di mana \(\Delta\) menggambarkan perubahan kecil namun finite (bukan infinitesimal).

Hukum Kedua Newton

Hukum kedua Newton menghubungkan gaya dengan gerak:

Kita dapat menggabungkan hukum gravitasi Newton dengan hukum kedua Newton:

Update Posisi dan Kecepatan

Dari percepatan, kita dapat menghitung posisi dan kecepatan baru:

⚖️ Akurasi dan Stabilitas Simulasi

Ada dua hal yang perlu dipilih dengan hati-hati:

1. Timestep (\(\Delta t\)) ⏱️

Untuk menjaga stabilitas simulasi. Timestep yang terlalu besar dapat menyebabkan simulasi menjadi tidak stabil dan hasil yang tidak akurat.

2. Jumlah Partikel (N) 🔢

Untuk resolusi simulasi. Semakin banyak partikel, semakin detail simulasi, tetapi semakin berat komputasinya.

Trade-off: Akurasi vs Computational Cost

🔄 The N-Body Algorithm

Berikut adalah algoritma dasar untuk simulasi N-body:

1. SET Kondisi Awal
   - N (jumlah benda)
   - Δt (timestep)
   - m (massa setiap benda)
   - r (posisi awal)
   - v (kecepatan awal)
   - F (gaya awal)

2. LOOP (untuk setiap timestep):
   a. Hitung gaya gravitasi pada setiap benda
      F_i = Σ G * m_i * m_j / r_ij²

   b. Selesaikan persamaan gerak
      a = Δv / Δt
      v = Δr / Δt

   c. Update posisi dan kecepatan
      v_new = v_old + a * Δt
      r_new = r_old + v * Δt

   d. Update time counter
      t_new = t_old + Δt

   e. Output data
      Simpan: r_new, v_new, F_new, t_new

3. REPEAT sampai waktu simulasi selesai

💡 Improving Algorithm

Your code, your modification = your novelty!

Penelitian komputasi astrofisika bukan hanya tentang menjalankan code yang sudah ada, tetapi meningkatkan dan memodifikasi algoritma untuk masalah spesifik yang Anda hadapi.

🌟 Kapan Komputasi Dibutuhkan dalam Astrofisika?

🪐 Dinamika Tata Surya

Menghitung orbit planet untuk jutaan tahun ke depan membutuhkan metode N-body yang sangat akurat.

⭐ Struktur dan Evolusi Bintang

Membutuhkan penyelesaian: - ODE (Ordinary Differential Equations) - Persamaan diferensial parsial - Aljabar linear - Hidrodinamika

🌌 Formasi Bintang dan Planet

Memerlukan kombinasi dari: - Hidrodinamika - MHD (Magnetohydrodynamics) - Metode N-body

✨ Dinamika Cluster Bintang

Membutuhkan metode N-body yang sangat cepat karena melibatkan ribuan hingga jutaan bintang.

🌠 Formasi Galaksi

Kombinasi dari: - Metode N-body yang sangat cepat - Hidrodinamika - Dark matter simulation

📊 Data Analysis & Image Processing

Memerlukan: - Aljabar linear - Pattern recognition - Data mining - Machine learning

🔮 Masa Depan Computational Astrophysics

Yang Pasti Terjadi:

Peningkatan performa hardware akan membuat problem yang lebih besar bisa ditangani secara numerik.

Yang Dibutuhkan:

1. Algoritma yang Lebih Akurat 🎯

Pengembangan metode numerik dengan error yang lebih kecil dan stabilitas yang lebih baik.

2. Community Code & Visualization 🛠️

Software open-source yang dapat digunakan dan dikembangkan oleh komunitas peneliti.

3. Fisika yang Lebih Realistis 🌌

Memasukkan lebih banyak fenomena fisika ke dalam simulasi: - Radiasi - Magnetic fields - Feedback processes - Dark matter dan dark energy

4. Generasi Baru Computational Astrophysicists 👨‍🔬👩‍🔬

Ini adalah masa depan yang sesungguhnya!

Mereka yang belajar komputasi sekarang akan menjadi peneliti yang memimpin revolusi dalam pemahaman kita tentang alam semesta.

🧠 Computational Thinking

Programming Bukan Hal yang Sulit

Programming bukan sesuatu yang susah untuk dipelajari dalam bentuk yang terstruktur, tetapi: - Akan susah jika terlalu bebas bentuknya (unstructured) - Lakukan lebih banyak daripada hanya mempelajari - practice makes perfect!

Belajar Algoritma

Banyak metode numerik relatif straightforward untuk dipelajari. Tentu saja ada pengecualian untuk algoritma yang kompleks, tetapi seringkali kita tidak membutuhkannya untuk penelitian dasar.

Filosofi Penelitian

"Algoritma adalah metode untuk mengerti yang mendasari masalah fisis. Jangan lupakan fakta kita sedang melakukan fisika, bukan hanya coding."

Menjadi peneliti yang baik dan efektif berarti mengetahui apa yang terjadi di belakang algoritma tersebut, bukan hanya menggunakannya sebagai black box.

Cara Terbaik Belajar Programming

Latihan lebih banyak daripada melihat/membaca!

"The best way to learn programming is by doing, not by watching."

📡 Big Data in Astronomy

Optical Astronomy: LSST

Large Synoptic Survey Telescope

• Kamera 32 gigapixels (setara 1500 layar HDTV!)
• Survey seluruh langit setiap tiga hari
• Data per hari = 3× Sloan Digital Sky Survey
• Total data katalog: 0.4 exabytes

Radio Astronomy: SKA

Square Kilometer Array

Menyimpan semua spectra line cubes membutuhkan 27 exabytes per tahun.

Tantangan: Technology dan cost problem yang sangat besar.

Masalah Analisis Data

Tidak hanya data besar yang bermasalah. Bahkan pada data kecil: - Klaim deteksi exoplanet yang tidak akurat - Perlu pendekatan statistik yang lebih sophisticated (Bayesian vs Frequentist) - Recognition yang melampaui pendekatan statistik sederhana

Tantangan Paradigma Baru: - Tekanan untuk publish membuat peneliti senior tidak punya banyak waktu untuk belajar tool baru - Secara alami, manusia ingin melanjutkan cara yang sudah mereka tahu - Ini adalah issue utama di berbagai field, tidak hanya astronomi

🎓 Kesimpulan

Computational astrophysics adalah bidang yang:

✅ Menggabungkan fisika, matematika, dan computer science
✅ Memungkinkan kita mempelajari fenomena yang tidak bisa diobservasi langsung
✅ Terus berkembang dengan teknologi baru
✅ Membuka peluang penelitian yang luar biasa

Kunci sukses: 1. Memahami fisika yang mendasari 2. Menguasai metode numerik 3. Kemampuan programming yang baik 4. Kreativitas dalam mengembangkan algoritma baru

📚 Referensi & Further Reading

• Binney, J., & Tremaine, S. - Galactic Dynamics
• Press, W. H., et al. - Numerical Recipes
• Hockney, R. W., & Eastwood, J. W. - Computer Simulation Using Particles
• Dehnen, W., & Read, J. I. - N-body simulations of gravitational dynamics

Course Notes - Dr. Hakim L. Malasan
IDEASOPHIA Astronomy Series

#Astrophysics #ComputationalAstronomy #NBodySimulation #Gravitation #NumericalMethods